16-Bit Atari Music
Fred Tedsen
Did you know that you can improve the tuning of your Atari's notes and extend its range dramatically? Normally you can only choose between 256 notes with the ordinary SOUND command. These subroutines let you have more than 65,000 frequencies to make music that's more precise and more pleasant to hear.
As I listened to my Atari play a new song that I had entered from a magazine listing, I could hear that some of the notes were not quite right. The music extended into the third octave above middle C, and though the tune was recognizable, some of the notes were off pitch enough to make listening to the tune unpleasant. I decided that it was time for me to investigate 16-bit music. What I discovered was not only that the accuracy of the notes could be improved dramatically, but also that the effective range could be more than doubled.
How SOUND Works
Before we discuss 16-bit music, let's take a look at what is happening when we use the SOUND statement or in other words, eight-bit sound, in Atari BASIC. The following registers in the POKEY chip are used for sound generation:
AUDF1 (53760) - Audio Frequency Register 1 AUDC1 (53761) - Audio Control Register 1 AUDF2 (53762) - Audio Frequency Register 2 AUDC2 (53763) - Audio Control Register 2 AUDF3 (53764) - Audio Frequency Register 3 AUDC3 (53765) - Audio Control Register 3 AUDF4 (53766) - Audio Frequency Register 4 AUDC4 (53767) - Audio Control Register 4 AUDCTL (53768) - Audio Mode Control Register
The audio control registers are used to set volume (low order four bits) and sound content (high order bits). Thus there are 16 different volume settings and a variety of sounds available. For this discussion we are concerned only with pure tones, corresponding to SOUND x,x,10,x.
The audio frequency registers are used to control the divide by "N" circuits. These circuits use the contents of the frequency registers to divide a "clock" frequency to produce different output frequencies. Since they are one-byte registers, they are referred to as eight-bit dividers. The output frequency is determined by the formula F0 = F/(2×(AUDF +1)), where F is the clock frequency and AUDF the value in the audio frequency register. With a normal clock rate of 64KHz(or more exactly 63,921 cycles per second), the frequency range is about 125Hz to 32KHz.
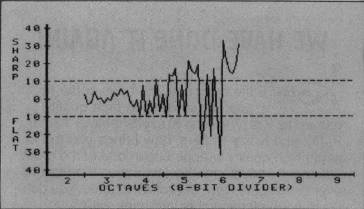
The effective range for music is limited to about four octaves. This is because the tuning accuracy of notes being reproduced becomes progressively worse as the frequency gets higher. Figure 1 illustrates this very clearly. It shows how far out of tune, measured in "cents," each note in the four octave range is. (A cent is l/100th of a half-step. A sound which is 50 cents sharp or flat is exactly half-way between two notes.) Notes which are less than ten cents out of tune are usually acceptable, though two notes played together could sound bad if their combined inaccuracy is too large. For example, if you play a note which is eight cents flat followed by a higher note which is eight cents sharp, the second note will probably sound out of tune.
Tuning inaccuracy results from having a limited number of values to use as dividers. With an eight-bit divider, only 256 unique frequencies can be reproduced. The A note in the fourth octave should be 440 cycles per second. To reproduce this note on the Atari, the number 72 is used as a divider. The resulting frequency is 437.8Hz, which is 8.6 cents flat. If instead we use 71 as a divider, the output frequency is 443.9Hz. This note is 15.3 cents sharp and is obviously a poorer choice than the note using 72. The choices become more restricted as the notes get higher. For the A note in the sixth octave, for example, 17 produces a note which is 15.3 cents sharp, while 18 produces a note 78.4 cents flat (closer to G# than A).
Fine-tuning: 16-Bit Dividers
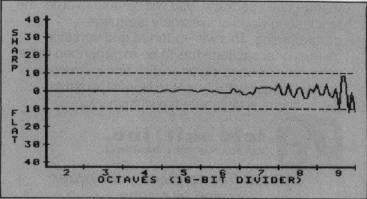
Luckily, the Atari provides a solution to this problem: 16-bit dividers. With a 16-bit divider 65,536 different output frequencies are possible. For example, to reproduce the A in octave 6, we could use either 502 (1.8 cents flat) or 501 (1.6 cents sharp) and not be able to hear any difference. Figure 2 shows how dramatically the range and accuracy are improved.
More accurate tuning does not come without a price. Sixteen-bit dividers are obtained by combining frequency registers: AUDF1 with AUDF2, or AUDF3 with AUDF4. This gives us a choice of one 16-bit and two eight-bit voices, or two 16-bit voices. We also cannot use the SOUND statement, even for the eight-bit voices, as it will confuse our settings for 16-bit sound. As it turns out, this is not much of a problem since machine language routines to play the music are simple and have the added advantage of being faster than separate SOUND statements.
|
Note Table.
|
Now let's look at how 16-bit sound is set up. The audio mode control register has four bits for this purpose:
Bit 6 — Clock channel 1 with 1.79MHz instead of 64KHz
Bit 5 — Clock channel 3 with 1.79MHz
Bit 4 — Combine channels 1 and 2
Bit 3 — Combine channels 3 and 4
The other bits in AUDCTL have no bearing on this discussion, so we will ignore them. If you are curious, see chapters 2 and 3 in the Hardware Manual.
The 1.79MHz (1.78979 MHz, to be exact) clock rate is required to obtain the full range of output frequencies. The formula for determining output frequency is a little different: F0 = F/(2×(AUDF + 7)). In this case, AUDF is the two-byte frequency register value. The second register of the pair is the low order byte, either AUDF2 or AUDF4. For example, to use 1049 as a divider with registers 1 and 2, we would POKE 4 in AUDF2 and 25 in AUDF1.
The audio control register of the low order frequency register is not used and should be set to zero. Volume is controlled with the second control register only (AUDC2 or AUDC4).
16-Bit Subroutines
Now take a look at the BASIC 16-bit sound subroutines. The first plays one 16-bit and two eightbit voices, and the second plays two 16-bit voices. Notice the SOUND 0, 0, 0, 0 at the beginning of each routine. This statement must be included to initialize POKEY for sound. The POKE 53768, X initializes AUDCTL for 16-bit sound, either one or two voices. Remember that any SOUND statement executed later will reset this register to zero.
To use these subroutines, simply copy one or the other into your program and do a GOSUB 20100 once at the beginning of the program. Then, to play music, do the appropriate machine language call, X = USR(ADR(HF1$), N1, V1, N2, V2, N3, V3)or X = USR(ADR(HF2$), N1, V1, N2, V2). Nx is the note to be played and Vx is the volume. N1 is the 16-bit voice in the three-voice routine. You don't need to pass parameters for unused voices. For example, if you want only the 16-bit voice in the three-voice routine, you can use X = USR(ADR(HF1$), N1, V1), but to use only an eight-bit voice you would have to use X = USR (ADR(HF1$), 0, 0, N2, V2).
The note tables give you the most accurate values for four octaves of eight-bit and nine octaves of 16-bit notes. In a practical sense, the first octave of 16-bit notes is not usable because there are some loud harmonics which tend to mask the actual note being played. You can get some good sounds if you hook up to a stereo amplifier, however. Notice that the eight-bit value for F# in the third octave is 172 rather than 173 as shown in the BASIC Reference Manual. 173 produces a note which is more than 12 cents flat, while the note from 172 is only 2.4 cents flat.
Finally, some thoughts on when to use 16-bit music. If you have a piece of music which sounds fine using SOUND in BASIC, don't bother changing it — you probably won't be able to hear much improvement. I think you'll find that just about any music which extends into the fifth octave will be worth converting, however, especially if it is very complex. For three-part music, use the 16-bit voice for the highest notes. Some chord combinations may still sound slightly out of tune, in which case you might want to tune the 16-bit voice a little sharp or flat to match the eight-bit voices. The large number of divider values available gives you plenty of possibilities.
Program 1.
20000 REM 16-BIT SOUND ROUTINE 1 20010 REM 20020 REM 1 16-BIT & 2 8-BIT VOICES 20030 REM 20040 REM X = USR(ADR(HF1$), N1, V1, N2, V2, N3, V3) 20050 REM 20100 SOUND 0, 0, 0, 0 : X = 64 + 16 : POKE 5376 8, X 20110 DIM HF1$(56) : RESTORE 20140 20120 FOR I = 1 TO 56 : READ X : HF1$(I, I) = CHR$(X): NEXT I 20130 RETURN 20140 DATA 104, 170, 104, 141, 2, 210, 104, 141, 0, 210, 104, 104, 41, 15, 9, 160, 141, 3, 210 20150 DATA 224, 2, 240, 32, 104, 104, 141, 4, 210, 104, 104, 41, 15, 9, 160, 141, 5, 210 20160 DATA 224, 4, 240, 14, 104, 104, 141, 6, 210, 104, 104, 41, 15, 9, 160, 141, 7, 210, 96
Program 2.
20000 REM 16-BIT SOUND ROUTINE 2 20010 REM 20020 REM 2 16-BIT VOICES 20030 REM 20040 REM X = USR(ADR(HF2$), N1, V1, N2, V2)20050 REM 20100 SOUND 0, 0, 0, 0 : X = (64 + 16) + (32 + 8) : POKE 53768, X 20110 DIM HF2$(41) : RESTORE 20140 20120 FOR I = 1 TO 41 : READ X : HF2$(I,I) = CHR$(X) : NEXT I 20130 RETURN 20140 DATA 104, 170, 104, 141, 2, 210, 104, 141, 0, 210, 104, 104, 41, 15, 9, 160, 141, 3, 210 20150 DATA 224, 2, 240, 17 20160 DATA 104, 141, 6, 210, 104, 141, 4, 210, 104, 104, 41, 15, 9, 160, 141, 7, 210, 96