TI Trapshoot

C. Regena

It's time to try your skill at the TI-99/4A trapshooting range. Each game consists of 50 clay pigeons sprung from the trap near the center of the screen. You aim the shotgun located at the bottom center of the screen by pressing the left or right arrow key. Fire when you are ready by pressing the ENTER key. You'll need to aim and fire quickly — you have only one chance per target.

At the lower right side of the screen is your scoring record. The number of successful hits, the number of clay pigeons, and the number of rounds fired are displayed.

Programming Techniques

Line 120 defines a function RRV for the random row velocity for the clay pigeon moving from 0 to 140 upward. You may change the number 14 in the equation to 15 or 16 to make the target move upward more quickly, but you will have less time to aim the shotgun, shoot, and hit the target.

Line 130 defines a function RCV for the random column velocity of -17 to +17 moving the target toward the left or right. The number 18 in the equation may be changed to decrease or increase the range of the target. Increasing the number will move the target more to the left or right, but the target may "wrap" to the other side of the screen before being deleted.

Following are the graphic representations of the seven positions of the shotgun:

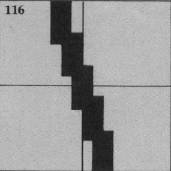
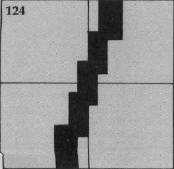
The shotgun is Sprite #3, defined in Line 190. There are seven shotgun positions drawn with characters 108 through 135. CALL MAGNIFY(4) is used so the shotgun may be drawn as large as possible by specifying only one character number for the sprite. If the left arrow key is pressed, the character number N is decreased by 4; if the right arrow key is pressed, N is increased by 4. N may vary from 108 to 132, where 120 is straight up. The shotgun position is changed after a key is pressed by using CALL PATTERN(#3,N).

Line 220 stops the game after 50 clay pigeons. You may change the limits of the game by changing the limit for T, or you may wish to test for the number of shots, SH (perhaps stopping after 50 rounds or 100 rounds instead of after 50 birds).

Line 230 springs the clay pigeon from the trap at the random row and column velocities. The target is Sprite #1.

If you press ENTER to fire, buckshot appears as Sprite #2 at the end of the shotgun and goes upward in the direction the shotgun is aimed. The value of N2 is N-120 and is used in calculating position and column velocity parameters for Sprite #2. The position of the end of the shotgun is dot column 116 plus some function of N2. Experimentation shows that the dot column position is 116 + N2*1.2.

By using trigonometry, the angle of the shotgun was determined dependent upon the character number. The ratio of the row velocity to the column velocity is equal to the ratio of the horizontal displacement to the vertical length of the shotgun. Whether the shotgun is pointing left or right is determined by SGN(N2). The upward (row) velocity of Sprite #2 was set at 100.

The theoretical factor to calculate column velocity is 12.5, but since the displacement per character number is not precisely linear, 12.7 works better. The resultant column velocity is (N2/4 + 2*SGN(N2))*12.7. I chose the row velocity of 100 so the buckshot moves faster than the clay pigeon, but slowly enough to report coincidence and to prevent wrapping on the screen.

Controlling Sprites

Lines 330-340 check to see if the buckshot hits the target. CALL COINC(ALL,C) is used so coincidence is reported if any dot of the buckshot coincides with any dot of the target. Using a statement such as CALL COINC(#1,#2, TOL,C) between two sprites tests coincidence of the upper left corners of each sprite within a certain tolerance; sometimes a hit would be scored when the buckshot appeared to miss the target.

The faster sprites move, the more difficult it is to control them in a program. Coincidence is reported only if the sprites are touching at the exact moment the CALL COINC statement is executed in the program. Once ENTER is pressed and the buckshot starts on its path, CALL COINC is executed in a FOR/NEXT loop 19 times. At the end of 19 loops without coincidence, the buckshot is near the top of the screen and is deleted.

If coincidence is reported, then the program branches to the appropriate section for a hit. If you change the speed of either the target or the buckshot, you may need to change the limit 19 in the FOR/NEXT loop. If you play many times, you may notice that once in a while the buckshot will pass through the target without recording a hit. This happens when the target is going straight upward slowly and you fire immediately. The sprites pass each other before the program has a chance to get to the CALL COINC statement. To avoid this problem, you could slow the buckshot down; however, I prefer the faster buckshot since the problem rarely occurs. This is an example of "programming trade-offs."

After the buckshot is deleted, the program keeps testing the position of the target until it is at the top of the screen; then Sprite #1, the target, is deleted (line 360). If ENTER is not pressed, then the position of Sprite #1 is tested in the CALL KEY loop.

If the target is hit, then the broken clay pigeon is shown by changing the pattern of the sprite. The buckshot disappears by changing the pattern of the buckshot to a blank character. The statement is CALL PATTERN(#1,100,#2,136). After sounding a hit using Noise -6, both sprites are deleted with CALL DELSPRITE(#1,#2).

99/4 Versus 99/4A

Note: Some of the consoles process at different rates. It makes a difference whether you have the TI-99/4, the earlier TI-99/4A, or the later TI-99/4A. It also makes a difference if you have the old Extended BASIC module or the new Extended BASIC. (You can tell which you have by holding a key down. If it will automatically repeat, you have a newer module.) Since this game is very critical on timing, you will have to experiment a little so that sprites won't wrap and cause bugs. You can adjust the game by changing the limit in line 330.

New XBASIC, TI-99/4A 330 FOR I = 1 TO 19 (or 20)
Old XBASIC, TI-99/4A 330 FOR I = 1 TO 9
New XBASIC, TI-99/4 330 FOR I = 1 TO 19
Old XBASIC, TI-99/4 330 FOR I = 1 TO 12